Solutions

Question

Each of 90 students participated at least 1 of the track tryouts: High jump, long jump, 100 meter dash. If 20 students participated in high jump tryout, 40 students participated in the long jump tryout and 60 students participated in the 100 meter dash tryout, and if 5 students participated in all 3 tryouts, how many students participated in only two of these tryouts?

 

Difficulty Level

Hard

Solution

Option B is the correct answer.

Option Analysis

Use Venn-Diagram for Non-Mutually Exclusive set type Questions:

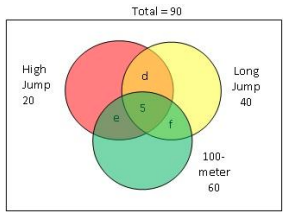
The high jump circle has 20 students. It includes the pink region (only High jump), d, e and 5 (students who tried all 3)

The long jump circle has 40 students. It includes the yellow region (only long jump), d, f and 5 (students who tried all 3)

The 100 meter dash circle has 60 students. It includes the green region (only 100 meter), e, f and 5 (students who tried all 3)

So when we add 20 + 40 + 60, you get 120 which is 30 more than 90. Why? Because in 20+40+60, we have counted, d, e and f twice and 5 thrice.

We need to subtract two times 5 and d+e+f once to get 90.

120 – 2*5 – (d+e+f) = 90

(d+e+f) = 20