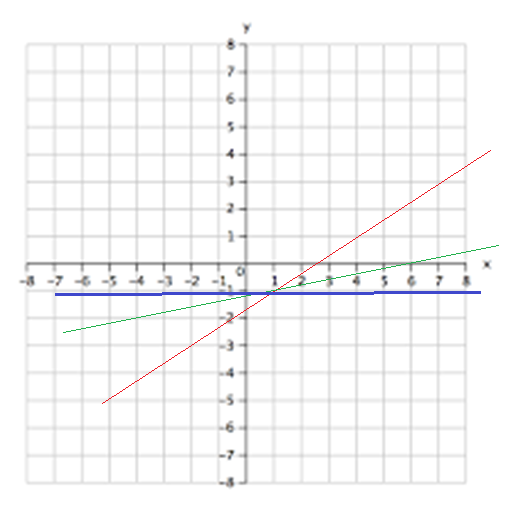
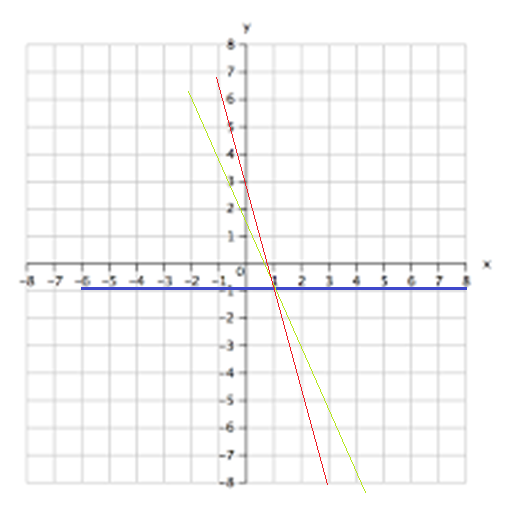
Where am I going wrong?
In the x y -plane, lines k and l intersect at the point (1,1). Is the y -intercept of k greater than the y -intercept of l ?
(1) The slope of k is less than the slope of l .
(2) The slope of l is positive.
If I draw the x-y plane and show 2 lines passing through (1,1) I can do that in various ways, depending on the slope. If I make them both positive, then both the statements together would be enough . However, if one of them is positive and one of them is negative, cant the one with the lower slope (i.e. negative slope) have a bigger y intercept depending on the value of the slope?!
Where am I going wrong?
Hi TC,
You have decided pretty early the conclusion of the question. Point(1,1) is given as the intersection and something about both the slopes is given in the statement I.
This is an easy question if you visualise,
Slope is the Increase in Y/ Increase in X………. OR Vertical increase / Horizontal increase..
If Both increase with increase in each other, the Slope is Positive.
But if Y decreases with increase in X, slope is negative.
So for a point (1,1), a line intercepting above Y as 1, it is negative slope and with increase in Y, the slope will have even lesser value.
At y=1, slope is 0 and at y<1, the slope will keep increasing as the value of Y increases…
So the relation of y-intercept is dependent on slope.. lesser the slope higher is the intercept..
Statement I is sufficient:
The slope of K is less than the slope of L.
As seen above y intercept of line l will be more than line k…
Sufficient.
(2) The slope of L is positive.
we require to know slope of line k also
Insufficient.
So the answer is A.
any decision made within 10 secs after reading is almost always wrong 🙂
thanks for the explanation.